Bloom Filters: A Comprehensive Guide

A bloom filter is a probabilistic data structure that is based on hashing. It is extremely space efficient and is typically used to add elements to a set and test if an element is in a set. However, the elements themselves are not added to a set. Instead, a hash of the elements is added to the set.

What is a Bloom Filter?

A Bloom filter is a space-efficient probabilistic data structure used to test whether an element is present in a set.
It was conceived by Burton Howard Bloom in 1970 as a solution to reduce the amount of storage needed for large sets while still providing fast query times.
Unlike traditional data structures like arrays or hash tables, Bloom filters do not store the elements. Instead, they use a bit array and hash functions to represent and check for the presence of elements.

How Does a Bloom Filter Work?

let’s see it in detail.

Bit Array initialization

A Bloom filter starts with an array of bits, typically denoted as B, with m bits initially set to 0.
The size m of the bit array is determined based on the expected number of elements to be added to the filter and the desired false positive rate.

Courtesy: GFG

Hash Functions:

A Bloom filter uses multiple independent hash functions, denoted as h1, h2, ..., hk, where k is the number of hash functions.
Each hash function maps an input element to one of the m positions in the bit array.

Adding Elements:

To add an element x to the Bloom filter:
1. Hash x using each hash function (h1(x), h2(x), …, hk(x)).
2. Set the corresponding bits in the bit array B to 1 at positions h1(x), h2(x), …, hk(x).

Checking for Membership:

To check if an element y is possibly in the set (may be a false positive), perform the following steps:
1. Hash y using each hash function (h1(y), h2(y), …, hk(y)).
2. Check if all the corresponding bits in B at positions h1(y), h2(y), …, hk(y) are set to 1.
  - If all bits are 1, y is considered “possibly in the set.”
  - If any bit is 0, y is not in the set.

Example

Let’s take an example with a bloom filter of 10-bit size and 3 hash functions.

With input as “geeks”

h1(“geeks”) % 10 = 1
h2(“geeks”) % 10 = 4
h3(“geeks”) % 10 = 7

Note: We took module(%10) as we have bloom filter of 10bits

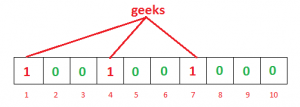
Courtesy: GFG

Suppose you want to check if “geeks” are present or not. Calculate the hash of input same as above and then check the indexes of the array. If all bits are set, then the input is probably present. If any of the bits at these indices are 0 then input is not present.

False positive and false negative

let’s delve deeper into the concept of false positives and false negatives

False Positives: In the context of Bloom filters, a false positive occurs when the filter incorrectly indicates that an element is part of the set, even though it was not added to the filter.

This can happen due to hash collisions, where multiple elements hash to the same positions in the bit array, leading to the setting of bits that may overlap with other elements.
False positives are inherent in probabilistic data structures like Bloom filters due to their space-efficient design and use of hash functions.

False Negatives: Conversely, a false negative occurs when the filter incorrectly indicates that an element is not part of the set, even though it was added to the filter.

In Bloom filters, false negatives are not possible. Once an element is added and hashed to set the corresponding bits in the array, the filter will never report that the element is not in the set unless those bits are later cleared (which is not supported in standard Bloom filters).

Comparison:

False positives are a concern in applications where the cost of an incorrect positive result is high (e.g., in security or critical data validation scenarios).
False negatives, while not applicable to Bloom filters, are significant in situations where missing an element from a set can lead to serious consequences (e.g., in medical diagnosis or financial transactions).

In summary, Bloom filters prioritize space efficiency and quick membership testing but trade off a small probability of false positives. False negatives are not possible in Bloom filters but are crucial considerations in other contexts where the absence of a true positive result can be problematic.

Probabilistic data structure

A Bloom filter is termed “probabilistic” because of its inherent probability-based nature when determining set membership. The probabilistic aspect arises due to two key factors:

1. False Positives:

When checking for the presence of an element in a Bloom filter, there is a possibility of false positives. This means that the filter may incorrectly report that an element is in the set, even though it may not have been added previously.
The probability of a false positive increases as the Bloom filter becomes more populated with elements and approaches its capacity, leading to potential collisions in hash functions.

2. Hash Functions:

Bloom filters use hash functions to map elements to positions in the bit array. These hash functions randomly distribute elements across the array, contributing to the probabilistic behaviour.
Since multiple elements can hash to the same bit positions (known as collisions), there is a chance that different elements may set the same bits in the array, leading to false positives during membership tests.

The probabilistic nature of Bloom filters is a trade-off for their space efficiency and fast membership testing. By allowing a small probability of false positives, Bloom filters can significantly reduce memory requirements compared to storing the actual elements. However, it’s crucial to consider this probability factor when designing systems that rely on Bloom filters, especially in applications where false positives are not acceptable.

How it’s space-efficient?

A Bloom filter is considered space-efficient due to its ability to represent a large set of elements using a relatively small amount of memory compared to storing the actual elements themselves. This space efficiency stems from several key factors:

1. Bit Array Representation:

Instead of storing the elements directly, a Bloom filter uses a bit array where each bit represents a position in the set.
The size of the bit array (m) is typically much smaller than the size of the actual set of elements, especially for large sets.

2. Hash Functions:

Bloom filters use multiple hash functions to map elements to positions in the bit array.
Since the hash functions distribute elements randomly across the array, each element only affects a few bits in the array.

3. Sparse Representation:

Initially, all bits in the bit array are set to 0. When elements are added, only specific bits corresponding to the hash values of the elements are set to 1.
This sparse representation means that a large set of elements can be represented using a small number of set bits in the array.

4. Constant Memory Usage:

The memory usage of a Bloom filter remains constant regardless of the number of elements added to it.
The size of the bit array (m) and the number of hash functions (k) are the primary factors that determine memory usage, not the size of the set being represented.

However, it’s essential to note that the space efficiency of Bloom filters comes with a trade-off, which is the probabilistic nature and the possibility of false positives. Due to collisions in hash functions, there can be instances where the filter incorrectly reports that an element is in the set (false positive). The acceptable false positive rate is typically determined based on the application’s requirements and the desired memory savings.

Operation on Bloom filter

insert(x): To insert an element in the Bloom Filter.
lookup(x): to check whether an element is already present in Bloom Filter with a positive false probability.

NOTE: We cannot delete an element in Bloom Filter

How to delete from the bloom filter?

Removing an element from this simple Bloom filter is impossible because there is no way to tell which of the k bits it maps to should be cleared.
Although setting any one of those k bits to zero suffices to remove the element, it would also remove any other elements that happen to map onto that bit.
Since the simple algorithm provides no way to determine whether any other elements have been added that affect the bits for the element to be removed, clearing any of the bits would introduce the possibility of false negatives.

Conclusion

In summary, Bloom filters offer a powerful and efficient way to manage membership queries in large data sets with a significant reduction in memory usage. Their probabilistic nature allows for quick lookups, making them ideal for applications such as web caching, network security, and database systems. While they may yield false positives, the trade-off is often acceptable given the substantial benefits in speed and storage efficiency. The use of multiple hash functions enhances their performance, but care must be taken to balance the number of bits allocated with the acceptable false positive rate. As data continues to grow in volume, Bloom filters present a valuable tool for optimizing resource management and enhancing system performance.