A tree is a fundamental data structure in computer science that simulates a hierarchical structure, much like a family tree. It consists of nodes connected by edges, with one node acting as the root, and the rest branching out into child nodes. Trees are widely used in various algorithms, databases, and file systems due to their efficient data representation and manipulation capabilities. In this article, we will explore the key concepts, types, and operations associated with trees.
Table of Contents
Basic Concepts
A tree is a collection of entities called nodes. These nodes are connected via edges. The relationships between nodes are established in a hierarchical structure, starting with a single root node, and branching into child nodes.
Key Terminology:
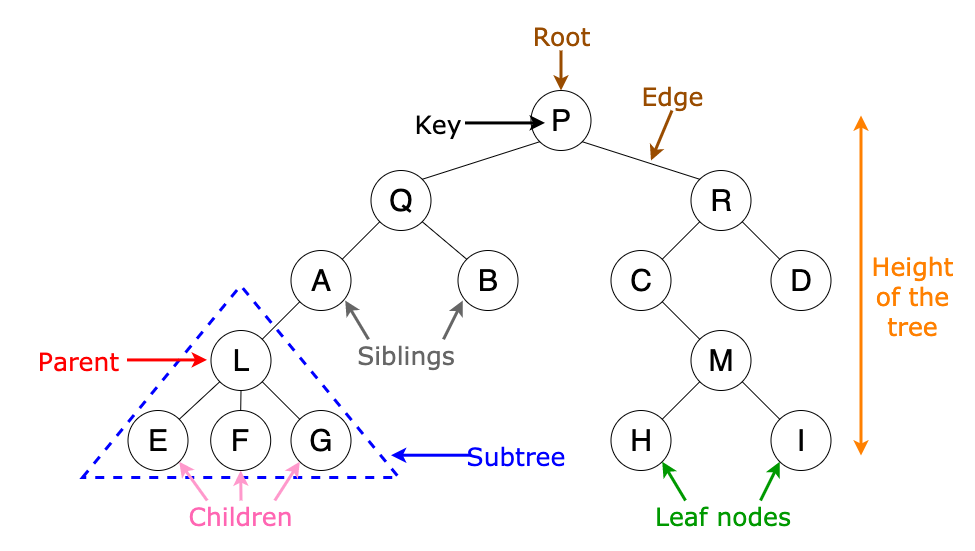
- Root: The topmost node in the tree. It has no parent node.
- Node: A fundamental part of the tree containing data and possibly links to child nodes.
- Edge: The connection between two nodes.
- Parent Node: A node that has one or more child nodes.
- Child Node: A node that descends from a parent node.
- Leaf Node: A node with no children.
- Subtree: A tree formed by a node and its descendants.
- Depth: The distance (number of edges) from the root node to a particular node.
- Height: The distance from a node to the deepest leaf in its subtree.
- Sibling: Nodes that share the same parent.
Properties of Trees
- Acyclic: Trees do not contain cycles. This means that there is no way to traverse from a node and come back to it by following the edges.
- Connected: All nodes in a tree are connected. There is a path between any two nodes in a tree.
- Single Root: Trees have only one root node. All other nodes are descendants of the root.
- N – 1 Edges: A tree with N nodes always has N−1 edges. This is a key property that differentiates trees from other graph structures.
Types of Trees
Binary Tree
A binary tree is a tree where each node has at most two children, referred to as the left child and the right child. This structure is frequently used in search algorithms and hierarchical data storage.
Properties:
- Each node can have 0, 1, or 2 children.
- Commonly used for binary search trees, heap structures, and expression trees.
Binary Search Tree (BST)
A Binary Search Tree is a type of binary tree where each node follows a specific ordering property: the left child of a node contains a value less than the node’s value, and the right child contains a value greater than the node’s value. This property makes searching, insertion, and deletion efficient.
Operations:
- Searching: O(h) where h is the height of the tree.
- Insertion and Deletion: O(h) on average, O(N) in the worst case.
Balanced Tree
A balanced tree is one where the height of the left and right subtrees of every node differs by no more than a certain factor (typically 1). Common examples include AVL Trees and Red-Black Trees.
Benefits:
- Ensures O(logN) time complexity for search, insertion, and deletion.
- Keeps the tree height minimal for efficient operations.
Heap
A heap is a special type of binary tree used in priority queues. Heaps maintain the property where the value of each node is greater (in a max-heap) or smaller (in a min-heap) than the values of its children.
Trie
A trie (pronounced “try”) is a type of tree used to store a dynamic set of strings. Tries are particularly useful for string manipulations like auto-completion and spell-checking.
Applications:
- Efficient string search operations.
- Often used in routing tables, text prediction systems, and word games.
Tree Representation
There are 2 main ways to represent trees :
Node-based
Node-Based (Object-Oriented) Representation
Each node is an object that stores:
- its value
- references to its children (usually left and right for binary trees)
Example
class TreeNode:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
# Example: Creating a tree manually
# 1
# / \
# 2 3
# /
# 4
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)This is the most common and preferred way in coding interviews and algorithm problems.
Dictionary/list
Using Dictionary or List (for Generic Trees or Trees with ID mapping)
This works when nodes are numbered or labeled and you’re given edges.
Example: Dictionary for N-ary Tree
tree = {
1: [2, 3],
2: [4, 5],
3: [],
4: [],
5: []
}
'''
1
/ \
2 3
/ \
4 5
'''Each key is a parent node; the list is its children.
When to Use Which?
| Use Case | Recommended Representation |
|---|---|
| Binary Tree / BST / LeetCode-style trees | Node-based with classes |
| N-ary Trees / Tree from edges | Dictionary/List adjacency model |
Tree Traversals
Tree traversal refers to visiting all the nodes of a tree in a specific order. There are two main types of tree traversal:
Depth-First Traversal (DFT)
DFT explores a tree by going as deep as possible down one branch before backtracking. The most common types are:
- Preorder (Root → Left → Right): Visit the root first, then the left subtree, followed by the right subtree.
- Inorder (Left → Root → Right): Visit the left subtree, then the root, and then the right subtree. This traversal yields sorted values in a binary search tree.
- Postorder (Left → Right → Root): Visit the left and right subtrees first, and then the root.
| Traversal Order | Visit Order |
|---|---|
| Inorder | Left → Root → Right |
| Preorder | Root → Left → Right |
| Postorder | Left → Right → Root |
Example
A
/ \
B C
/ \
D E
Inorder Output: D B E A C
Preorder Traversal: A B D E C
Postorder Traversal: D E B C A Inorder Traversal (Left → Root → Right)
def inorder(node):
if node:
inorder(node.left)
print(node.val)
inorder(node.right)Use Case: BSTs (Binary Search Trees). Inorder traversal gives nodes in sorted order.
Preorder Traversal (Root → Left → Right)
def preorder(node):
if node:
print(node.val)
preorder(node.left)
preorder(node.right)Use Case: Copying or serializing a tree (e.g., for saving to disk). Root is always visited first.
Postorder Traversal (Left → Right → Root)
def postorder(node):
if node:
postorder(node.left)
postorder(node.right)
print(node.val)Use Case: Deleting/freeing a tree, evaluating expressions (in expression trees).
Complete Code
class Node:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
# Sample Tree Creation
# A
# / \
# B C
# / \
# D E
root = Node('A')
root.left = Node('B')
root.right = Node('C')
root.left.left = Node('D')
root.left.right = Node('E')
# DFS Traversal Functions
def inorder(node):
if node:
inorder(node.left)
print(node.val, end=' ')
inorder(node.right)
def preorder(node):
if node:
print(node.val, end=' ')
preorder(node.left)
preorder(node.right)
def postorder(node):
if node:
postorder(node.left)
postorder(node.right)
print(node.val, end=' ')
# Run all three DFS traversals
print("Inorder Traversal:")
inorder(root) # Output: D B E A C
print("\nPreorder Traversal:")
preorder(root) # Output: A B D E C
print("\nPostorder Traversal:")
postorder(root) # Output: D E B C A
DFS Traversal Variants
You can implement DFS recursively (as above) or iteratively using a stack.
class TreeNode:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
def inorder_iterative(root):
stack = []
current = root
result = []
while current or stack:
# Reach the leftmost node
while current:
stack.append(current)
current = current.left
current = stack.pop()
result.append(current.val) # Visit root
current = current.right
return result
def preorder_iterative(root):
if not root:
return []
stack = [root]
result = []
while stack:
node = stack.pop()
result.append(node.val) # Visit root
# Right is pushed first so left is processed first
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return result
def postorder_iterative(root):
if not root:
return []
stack = [root]
result = []
while stack:
node = stack.pop()
result.append(node.val) # Reverse Root → Right → Left
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return result[::-1] # Reverse to get Left → Right → Root| Approach | Extra Space | Reversal Needed | Intuition |
|---|---|---|---|
| Single stack + reverse | 1 stack | Yes | Faster to implement |
| Two stacks | 2 stacks | No | More intuitive for postorder |
Breadth-first traversal (BFT)
Also known as level-order traversal, this method visits nodes level by level from left to right. It uses a queue to traverse the tree layer by layer.
It explores all the nodes at the present depth level before moving on to the next level.
Where is BFS used?
- Shortest path in unweighted graphs (like in a maze)
- Level order traversal of trees
- Finding connected components in graphs
- Crawling websites (like search engines)
- AI/game logic (like in chess)
How it works?
It uses a queue (FIFO) to keep track of nodes to visit next.
Steps:
- Start from a node (usually the root or source).
- Push it into a queue and mark as visited.
- While the queue is not empty:
- Dequeue a node current
- Visit all its unvisited neighbors/children
- Enqueue them and mark as visited
A
/ \
B C
/ \ \
D E F
BFS : A → B → C → D → E → FExample
from collections import deque
class Node:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
def bfs_tree(root):
if not root:
return
queue = deque([root])
while queue:
node = queue.popleft()
print(node.val, end=' ')
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
# Build a tree:
# 1
# / \
# 2 3
# / \
# 4 5
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
bfs_tree(root) # Output: 1 2 3 4 5
BFS vs DFS
| Feature / Aspect | BFS (Breadth-First Search) | DFS (Depth-First Search) |
|---|---|---|
| Traversal Strategy | Level by level (breadth-first) | Depth-wise (deep first) |
| Data Structure Used | Queue (FIFO) | Stack (LIFO) or recursion |
| Implementation Style | Iterative | Recursive or Iterative |
| Traversal Order | Horizontal | Vertical |
| Best for Shortest Path (Unweighted) | Yes | No |
| Tree Traversals (Pre/In/Post-order) | No | Yes |
| Level Order Traversal | Yes | No |
| Cycle Detection (Directed Graphs) | Possible, but not typical | Commonly used |
| Topological Sort | Not suitable | Yes |
| Space Complexity | O(V) — due to queue | O(V) — due to recursion/stack |
| Time Complexity | O(V + E) | O(V + E) |
| Memory Usage (in Wide Graphs/Trees) | Can be high (many nodes per level) | Usually lower (follows one path) |
| Good for Very Deep Graphs | No (space intensive) | Yes |
| Path Existence Check | Yes | Yes |
| Finding Connected Components | Yes | Yes |
| Common Use Cases | Shortest path, level order traversal | Topological sort, cycle detection, backtracking |
| Recursion-Friendly | No | Yes |
Common Operations on Trees
- Insertion: Adding a node to the tree while maintaining the specific ordering properties of the tree (e.g., binary search property for BSTs).
- Deletion: Removing a node and reorganizing the tree to maintain its structure and properties. Deletion in a binary search tree has three cases:
- Node is a leaf (no children).
- Node has one child.
- Node has two children (requires finding the in-order predecessor or successor).
- Searching: Finding a node with a particular value, with the efficiency depending on the type of tree (e.g., O(logN)O(\log N)O(logN) in balanced BSTs).
- Balancing: Adjusting the structure of the tree to ensure that the height remains small. This is crucial for maintaining efficient operations.
Applications of Trees
Trees are used in a wide range of real-world applications, including:
- File Systems: The hierarchical organization of directories and files is modeled as a tree.
- Databases: B-trees and B+ trees are used in databases for indexing to ensure efficient data retrieval.
- Compiler Design: Abstract syntax trees represent the structure of program code for compilers and interpreters.
- Artificial Intelligence: Decision trees are a popular method for decision-making processes in machine learning and AI.
- Networking: Routing algorithms often use spanning trees to determine the best paths in networks.
Conclusion
Trees are one of the most versatile and essential data structures in computer science. Their hierarchical nature and efficiency make them ideal for storing and manipulating structured data. Understanding tree operations and their various types is crucial for software developers, as trees are foundational in algorithms, databases, and many real-world applications. Whether it’s building a binary search tree for quick data lookups or leveraging a trie for efficient string operations, trees remain a powerful tool in a developer’s toolkit.
1 thought on “Understanding the Tree Data Structure”