Matrices are fundamental data structures in computer science and mathematics. In competitive programming, matrices are widely used in problems involving 2D grids, dynamic programming, graph algorithms, geometry, and simulations.
Table of Contents
Basics of Matrices in Python
Python doesn’t have a native matrix type. A matrix is typically represented as a list of lists:
# 3x3 Matrix
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
# Access elements:
print(matrix[0][1]) # Output: 2 (1st row, 2nd column)
# Modifying elements:
matrix[1][1] = 9
Concepts
Matric Representation
m*n matric
m: number of row
n: number of columnInitialisation Tricks
Zero Matrix (m x n)
# m : row
# n : col
matrix = [[0 for _ in range(n)] for _ in range(m)]
or
matrix = [[0] * n for _ in range(m)] Avoid [[0]*m]*n, as it creates shallow copies.
- [0] * 3 creates a single list: [0, 0, 0]
- Wrapping it with * 3 duplicates the reference to this same list three times.
So, matrix becomes:
[
[0,0,0],
[0,0,0],
[0,0,0]
]But internally, all three sublists are the exact same object in memory.
Identity Matrix (n x n)
A square matrix where the diagonal elements are all 1, and all other elements are 0
def identity_matrix(n):
return [[1 if i == j else 0 for j in range(n)] for i in range(n)]
print(identity_matrix(4))
#[[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]Matrix size: m(row) * n(col)
m = len(matrix) # number of rows
n = len(matrix[0]) # number of columnsZip Function
print(list(zip([1, 2, 3], [4, 5, 6],[7, 8, 9])))
# [(1, 4, 7), (2, 5, 8), (3, 6, 9)]
for pair in zip([1, 2, 3], [4, 5, 6],[7, 8, 9]):
print(pair)
'''
Output
(1, 4, 7)
(2, 5, 8)
(3, 6, 9)
'''* Operator
The * operator unpacks the list into individual arguments.
print(*[1,2,3]) # 1 2 3
print(*[[1,2,3]]) # [1, 2, 3]Example
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
print(matrix) # [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
print(*matrix) # [1, 2, 3] [4, 5, 6] [7, 8, 9]
zip(*matrix) => zip([1, 2, 3], [4, 5, 6], [7, 8, 9])
'''
Output
(1, 4, 7)
(2, 5, 8)
(3, 6, 9)
'''When you write:
zip(*matrix)It’s equivalent to:
zip(matrix[0], matrix[1], matrix[2], ..., matrix[n-1])
— assuming matrix has n rows.Traversal Techniques
Standard Traversal (Row-wise)
matrix = [
[1,2,3,4],
[5,6,7,8]
]
m = len(matrix)
n = len(matrix[0])
for i in range(m):
for j in range(n):
print(matrix[i][j],end=" ")
print()
'''
1 2 3 4
5 6 7 8
'''
for row in matrix:
for elem in row:
print(elem, end=' ')
print()
'''
1 2 3 4
5 6 7 8
''' 4-directional movement (for BFS/DFS)
dirs = [(-1, 0), (1, 0), (0, -1), (0, 1)]is defining a list of direction vectors used for moving in four directions on a 2D grid:
- (-1, 0) → up
- (1, 0) → down
- (0, -1) → left
- (0, 1) → right
Why use it?
In grid-based problems (like pathfinding, flood fill, maze traversal), you’ll often need to visit neighboring cells. This list helps you write concise and clean code in loops:
for dx, dy in dirs:
nx, ny = x + dx, y + dy
if 0 <= nx < n and 0 <= ny < m:
# process neighbor (nx, ny)It avoids repetitive code and keeps movement logic centralized.
8-directional movement (with diagonals)
dirs8 = [(-1, -1), (-1, 0), (-1, 1),
( 0, -1), ( 0, 1),
( 1, -1), ( 1, 0), ( 1, 1)]What is this?
This defines movement vectors that let you move in all eight directions from a cell in a 2D grid:
| Direction | Vector |
|---|---|
| Top-left | (-1, -1) |
| Top | (-1, 0) |
| Top-right | (-1, 1) |
| Left | (0, -1) |
| Right | (0, 1) |
| Bottom-left | (1, -1) |
| Bottom | (1, 0) |
| Bottom-right | (1, 1) |
Why use it?
In problems where you need to check diagonal neighbors as well (like detecting adjacent cells in Minesweeper or connected components), you need 8-directional movement.
Example Use Case
Let’s say you’re trying to count the number of connected components (or “islands”) in a grid, and diagonals count as connected:
def dfs(grid, x, y, visited):
n, m = len(grid), len(grid[0])
visited[x][y] = True
for dx, dy in dirs8:
nx, ny = x + dx, y + dy
if 0 <= nx < n and 0 <= ny < m:
if grid[nx][ny] == 1 and not visited[nx][ny]:
dfs(grid, nx, ny, visited)Standard Operations
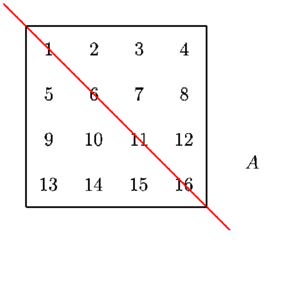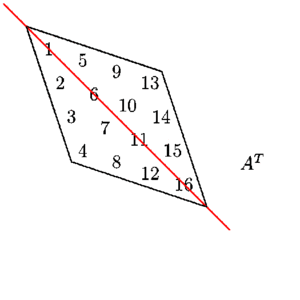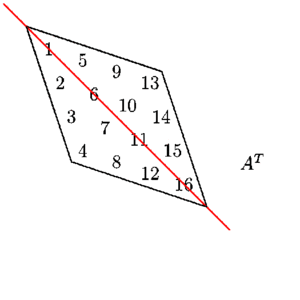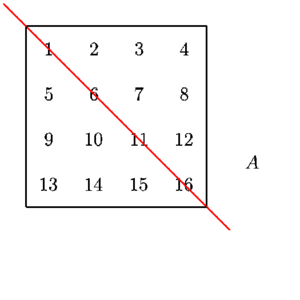
Matrix Transpose
The transpose of a matrix is the matrix flipped over its main diagonal, switching the matrix’s row and column indices.
- Matrix : m*n
- Transposed matrix(n*m)
[[1,2],
[3,4],
[5,6]
]
Transpose
[[1, 3, 5],
[2, 4, 6]]
def transpose(matrix):
m = len(matrix) # Number of rows
n = len(matrix[0]) # Number of columns
result = [[0] * m for _ in range(n)] # Transposed matrix: n x m
for i in range(m):
for j in range(n):
result[j][i] = matrix[i][j]
return result
matrix = [
[1, 2, 3],
[4, 5, 6]
]
transposed = transpose(matrix)
for row in transposed:
print(row)
'''
Output
[1, 4]
[2, 5]
[3, 6]
''' result = [[0] * m for _ in range(n)] # matrix : m*n then transposed matrix n*mUsing inbuit zip function
def transpose(matrix):
return [list(row) for row in zip(*matrix)]- it will work for any m*n matrix
- This is not a in_place operation
In-Place Transpose for Square Matrix
In-memory (in-place) transpose is possible, but only for square matrices — meaning the matrix has the same number of rows and columns (e.g., 3×3, 4×4, etc.).
For non-square matrices, transposition changes the dimensions, so it cannot be done truly in-place unless you change the data structure itself (which usually defeats the point).
def transpose_in_place(matrix):
n = len(matrix)
for i in range(n):
for j in range(i + 1, n):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]How It Works?
You’re swapping matrix[i][j] with matrix[j][i] only for i < j to avoid undoing previous swaps or swapping the diagonal with itself.
Swapping
Traversing (01,02,03,12,13,23) enough to swap
This way, it runs in O(n²) time and O(1) space.
Example
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
transpose_in_place(matrix)
for row in matrix:
print(row)
'''
[1, 4, 7]
[2, 5, 8]
[3, 6, 9]
'''Matrix Multiplication
def multiply_matrices(A, B):
n, m, p = len(A), len(B), len(B[0])
result = [[0] * p for _ in range(n)]
for i in range(n):
for j in range(p):
for k in range(m):
result[i][j] += A[i][k] * B[k][j]
return result
Matrix Rotation
Concept 1 : Index Flip
Suppose we have array of length(n) it’s index will be 0,1,2,3…n-1
my_array = [1,2,3,4,5,6]
flip/reverse it
my_array = [6,5,4,3,2,1]Index
Index
0 -> n-1 -> n-1 - 0
1 -> n-2 -> n-1 - 1
2 -> n-3 -> n-1 - 2
3 -> n-4 -> n-1 - 3
..
..
n-2 -> 1 -> n-1 - (n-2)
n-1 -> 0 -> n-1 - (n-1) So the general formula to flip the array will be n-1-i
my_array = [1,2,3,4,5,6]
n = len(my_array)
new_array = [0]*n
for i in range(n):
new_array[n-1-i] = my_array[i]
print(new_array) # [6, 5, 4, 3, 2, 1]Concept 2 : Rotation
matrix = [
[1, 2],
[3, 4],
[5, 6]
]
# rotate_90 clockwise
matrix = [
[5, 3, 1],
[6, 4, 2],
]
# rotate_180 clockwise
matrix = [
[6, 5],
[4, 3],
[2, 1]
]matrix = [
[1, 2],
[3, 4],
[5, 6]
]
# rotate_90 counter clockwise
matrix = [
[2, 4, 6],
[1, 3, 5],
]
# rotate_180 counter clockwise
matrix = [
[6, 5],
[4, 3],
[2, 1]
]Note : 180′ for both clockwise and counter clockwise give same result
Concept 3 : Transpose plus reverse
matrix = [
[1, 2],
[3, 4],
[5, 6]
]
# Transpose
matrix = [
[1, 3, 5],
[2, 4, 6]
]
# rotate_90 clockwise
matrix = [
[5, 3, 1],
[6, 4, 2],
]
- Transpose and then we reverse the row => 90′ clockwise
- (i,j) -> (j,n-1-i)
matrix = [
[1, 2],
[3, 4],
[5, 6]
]
# Transpose
matrix = [
[1, 3, 5],
[2, 4, 6]
]
# rotate_90 counter clockwise
matrix = [
[2, 4, 6],
[1, 3, 5],
]- Transpose and then we reverse the column => 90′ counter clockwise
- (i,j) -> (n-1-i,j)
Summary
| Rotation Direction | Steps |
|---|---|
| Clockwise | Transpose → Reverse each row |
| Counter-Clockwise | Transpose → Reverse each column |
Clockwise 90′ rotation
def rotate_clockwise(matrix): # m*n
m = len(matrix) # original rows
n = len(matrix[0]) # original cols
rotated = [[0] * m for _ in range(n)] # n*m
for i in range(m):
for j in range(n):
rotated[j][m - 1 - i] = matrix[i][j]
return rotatedIn place operation, it possible only for square matrix
Way 1
def rotate(matrix):
n = len(matrix)
# Step 1: Transpose
for i in range(n):
for j in range(i + 1, n):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
# Step 2: Reverse each row
for row in matrix:
row.reverse()
return matrixWay 2:
def rotate_90(matrix):
return [list(reversed(col)) for col in zip(*matrix)]
Counter Clockwise 90′ rotation
def rotate_counterclockwise(matrix):
m = len(matrix)
n = len(matrix[0])
rotated = [[0] * m for _ in range(n)]
for i in range(m):
for j in range(n):
rotated[n - 1 - j][i] = matrix[i][j]
return rotated
In place operation, it possible only for square matrix
Way 1
def rotate_90_counterclockwise(matrix):
n = len(matrix)
# Step 1: Transpose
for i in range(n):
for j in range(i + 1, n):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
# Step 2: Reverse each column
for j in range(n):
for i in range(n // 2):
matrix[i][j], matrix[n - 1 - i][j] = matrix[n - 1 - i][j], matrix[i][j]Rotate Matrix 180° (Any Size)
- Rotating a matrix 180° is equivalent to reversing both the rows and the elements inside them.
- Clockwise and counter clockwise both is same
def rotate_180(matrix):
return [row[::-1] for row in matrix[::-1]]
Horizontal Flip (Mirror over vertical axis)
Each row is reversed — like flipping left ↔ right.
def flip_horizontal(matrix):
return [row[::-1] for row in matrix]
Vertical Flip (Mirror over horizontal axis)
Just reverse the order of rows — like flipping top ↔ bottom.
def flip_vertical(matrix):
return matrix[::-1]
Example
matrix = [
[1, 2, 3],
[4, 5, 6]
]
print("180° Rotation:")
for row in rotate_180(matrix):
print(row)
print("\nHorizontal Flip:")
for row in flip_horizontal(matrix):
print(row)
print("\nVertical Flip:")
for row in flip_vertical(matrix):
print(row)
Output
180° Rotation:
[6, 5, 4]
[3, 2, 1]
Horizontal Flip:
[3, 2, 1]
[6, 5, 4]
Vertical Flip:
[4, 5, 6]
[1, 2, 3]
Conclusion
Matrices are powerful tools in the competitive programmer’s toolkit. Whether for pathfinding, simulations, or dynamic programming, understanding how to manipulate and optimize matrix operations in Python is essential for tackling a wide variety of problems.
1 thought on “Complete Guide to Matrices”